Pulsed Magnets: Ever thought of building a magnet on your own which would sit on a table-top and give you a field as high as 20 tesla? If you don’t have any idea on how big a 20 T magnetic field is, let me tell you that a field of 4-5 T, if kept ON at your vicinity for some time, can start pulling tables and chairs and maybe you as well if you are sitting on the chair! But don’t worry, this 20 T won’t have much energy to do so since it would last only for a few milliseconds. That’s why what I want to discuss now are called “Pulsed Magnets”, i.e. the magnetic field would come in burst of a pulse and then would die down quickly before causing any physical disturbances. But if you are talking about disturbances caused to the electrons in a semiconductor at low temperatures, as in Quantum Hall Effect, or to the excitons in, say, Carbon Nanotubes, as in magneto-optical spectroscopy, the ‘ms’ (millisecond) pulses would be sufficient because these quantum particles will, more often than not, have a response time which is much less than a millisecond! This means though your magnetic field is lasting for a few ‘ms’, you are still getting to probe the state of a particle in your sample once it has reached “equilibrium” in the magnetic field!
An interesting point to consider is, it is because of the fact that the magnetic field lasts for less than a second, can these magnets be at all constructed on a table-top! A standard wire-wound DC electromagnet cannot give you a field more than 3 T – considering you have a minimum of 2 cm by 2 cm free space carrying that magnetic field (for your own access: usually used to mount your sample)! If you want higher fields you can go to a standard 10-12 T superconducting magnet. But superconducting magnets have standard hazards of running with liquid Helium (can take you down to 4K) which is costly and less readily available compared to other cheaper cryogenic coolers like Liquid Nitrogen (can take you down to 77K). The regular use of liquid Helium is what which makes superconducting magnets less accessible to the common man: we usually have “Central (means belonging to the National Government) Facilities” that run such magnets. Why is it difficult to get a high magnetic field that lasts for a long time?
Now, whatever value of the magnetic field you are aiming at, you should have a proportional value of current flowing through your magnet: a high current gives you a high field. Whenever you pass a high current through a coil of wire (the solenoid) there will be heating effects – which, if you are having no control of, might finally end up burning your magnet! As the Joule heat goes as: Q = I2Rt, minimizing ‘t’ (i.e. the time for which the current ‘I’ is flowing) helps you to push a very high current (in kilo or Mega Amps) through your magnet. This is the principle behind a “pulsed magnet”.
The Magnet Coil: Let me show you how the magnet coil would look. The solenoid represents a multilayer winding of copper wire and so, after the magnet is tightly “wound”, the coil will have a tendency of falling off if it’s not properly held in place! So, you would first require a skeleton that can mechanically hold your coil. I will tell you how we do it in our lab.
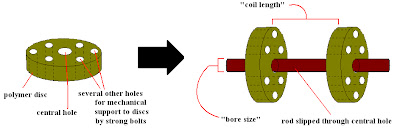
Take a sturdy polymer disc (like nylon or polypropylene, even Teflon would do) and drill holes through it as shown above. And then take 2 such discs and slip a rod through their centers. Be careful of the distance you fix between the 2 polymer discs (along the central rod: i.e. along the magnet axis). This will be referred to as the “coil length” or ‘2b’. The diameter of the “central hole” would be referred to as the “bore size” of the magnet. This represents, ‘area’-wise, the total space you will get to place your “sample” in the field. Mind it that the solenoid is an “air-core” one, i.e. the coil, unlike standard electromagnets, is not wound round an iron core. Later, when coil winding is over, you would be slipping the central rod out – which will give you a cylindrical hole at the centre of the 2 parallely placed discs. This space will carry the field and the diameter of this cylinder will be the “bore size”. Take it as: ‘2a1’, i.e. the bore radius is ‘a1’. You might well ask: why not fill up the air gap with a soft-iron core and get some more field! Since magnetic field would go as: B = [μ*(N/L)]*I, where ‘N/L’ is “the # of turns per unit length of the solenoid”, increasing magnetic permeability (μ) would increase the field right? Wrong! Because permeability saturates at such high magnetic fields (10s of Teslas): so it wouldn’t make much of a difference. Further, as I will show you soon, the magnetic field becomes half at the coil edge compared to what it is at the centre of the air-core! So filling the space up with something will stop your samples from accessing the bore space, i.e. the maximum field. Now this configuration of “mounting” your samples refers to the use of an “axial” geometry rather than the “transverse” one (as practised in the configuration of, say, a “Helmholtz Coil”): i.e. your sample, which you want to place in a 20 T field, needs to be placed on the head of a cylindrical rod that would go inside the air-core and sit at the centre of the coil.
Now, coming back to the magnet design, once the skeleton is ready, you need to start winding the copper wire around the central rod. The process, very crudely speaking, resembles something like this:
Now, an important point. Be careful of the diameter of the copper wire that you use for winding. This diameter will be referred to as the “winding wire diameter” or ‘wd’ and you will see how crucially its value would determine the “geometry of the coil”, i.e. the magnetic field : current conversion ratio (which is fixed for a given solenoid once the winding is complete). You can go ahead and choose commonly available copper wire gauges in the market, e.g. “SWG 17” which would mean a copper wire of ~ 1.4 mm “bare dia”. The “insulated dia” can be slightly more: this is because the wire will be coated with a typical layer of varnish. We will refer to the insulated dia as: “wd”. The bare dia will be referred to as: (λ*wd), where λ is called “Filling Fraction” or sometimes the “Space Factor”. It represents what fraction of the total wire volume is ‘conducting’, i.e. can effectively carry current. A question can arise: why do we need to use copper? Won’t any other material do? Actually, any good electrical conductor will do. Best choices are copper or aluminium since they are cheap and readily available. Copper is preferred to aluminium because of its higher electrical conductivity. Resistance of the coil would depend on this and so would the peak current that can be pushed by a given discharging circuit. We would discuss the discharging circuit when we finish discussing the Magnet Coil. Refer to the resistivity of the coil material (e.g.- copper) to be “ρ(T)”. As you can see, it depends on the temperature of the coil. Sometimes the entire magnet can be immersed in some cryogen, say, Liquid Nitrogen. This reduces the resistivity and thus the coil resistance by a factor of 8! This enables us to push more current still.
Coming back, one piece of suggestion would be: to never wind your coil with a wire which is bare/ not-insulated: current will short through the adjacent loops of the inductor rather than flowing directly through each of them. However, for people who know what inductors are this is obvious! While winding the coil you wind the wire loops tightly – placing each loop adjacent to its neighboring loop – going on winding from the end of one disc to another, all along the length ‘2b’. So number of turns will be: (2b/wd). Now after winding the first “layer” you can similarly wind the second by placing it on top of the first, and thus onwards the third layer by placing it on top of the second. This is what is generally referred to as a “multilayer winding”. So the total number of turns, taking into account all the layers, will be: “# of layers” * “# of turns per layer = (2b/wd)”. Take the total number of turns to be “N”. So after coil winding is complete, it would look somewhat like this:
Now, since the winding would have a tendency of coming off owing to its stored elastic (potential) energy, you may put some Araldite and Mseal to hold the coil in place. Then slip the central rod out after the glue has dried completely. Just as ‘a1’ can be called the “inner coil radius”, ‘a2’ can be called the “outer coil radius”; ‘a2’ = a1 + (“# of layers in the winding” * ‘wd’). One more step is essential for completing the construction of the Magnet Coil. Now,any conductor carrying a high current and placed in a high magnetic field will undergo “mechanical vibrations” due to “Lorentz forces”. These vibrations, unless dampened out, can cause unnecessary trouble to your sample, sitting deep inside the bore of the magnet. A standard way to minimize this is to use sturdy bolts that can now be slipped through the extra holes on the 2 discs. Later you can go ahead to “clamp” the entire magnet to some heavy mechanical support by using these bolts and some nuts.
So, if you would conceptually subtract, now, the “skeleton” from the entire magnet assembly, you would get the solenoid:
For all future calculations, we would take the “Normalized Coil Parameters”: α = (a2/a1), β = (b/a1) instead of taking ‘a2’ and ‘b’.
Let’s conclude the ongoing discussion by telling you how widely field varies along the axis of a solenoid. Magnetic field is maximum at the centre of the solenoid: i.e. deep inside the bore, at a distance ‘b’ from the coil edge. It drops off rapidly as one approaches the Coil Edge. The schematic follows below.
The interesting fact to note is: the field drops down to almost half at the coil-edge! At the edge of the nylon-disc, it would drop down to 1/10th of its central value! This is just to show you why it’s important to drop your sample all the way down to the centre of the bore rather than trying to access the field at the edge or on the surface of the polymer disc. This again validates our idea of using an air-core Coil.
The Discharging Circuit: Now, given that the magnet is ready, let’s see how we can push a very high current through it for a very short time. The magnet is nothing but an inductor. The expression for the “Coil Inductance” ‘L’ of a multilayer air-core winding is: L = a1*N2*χ(α,β), where χ(α,β) is called the “Inductance Geometry Factor” , which, for all practical purposes (for each of α and β varying between 1 and 10), varies between 10-9 to 10-7, considering a1 is measured in ‘cm’ and L is measured in ‘Henry’. However, we must remember that the magnet has some resistance ‘R’ as well! The “Coil Resistance” is easy to calculate. The mean radius of the turns is the mean of the inner and outer radius, i.e. rmean = (a1+a2)/2. Mean length of one turn, thus, will be Lmean = 2πrmean. The total length of wire spent for winding the magnet coil is: L = N*Lmean. The total cross-section of the magnet = 2b*(a2-a1).
The total magnet cross-section through which current would effectively flow = 2b*(a2-a1)*λ. This is because each turn is insulated from its neighboring turn (with a filling fraction = λ) as mentioned earlier. Since ‘N’ number of turns pass through this cross-section, we say, effective area through which the magnet current flows is: Amean = [2b*(a2-a1)*λ]/N. The resistance of the magnet winding can thus be calculated as: R = ρ*Lmean/Amean. This comes down to: R = [(ρ*N2)/(λ*a1)]*[{π*(α+1)}/{2β*(α-1)}]. So the Coil-Inductance ‘L’ remains in series with this Coil-Resistance ‘R’.
There are many ways in which a very high current can be pushed through a series R-L circuit within a fraction of a second. One of the commonly practiced ones is a Capacitive Discharge. You connect a capacitor bank of capacitance ‘C’ in series with the magnet. This makes a series R-L-C circuit. The aim is to electrically short the capacitor bank with the Magnet Coil once the bank has been charged to a desired high voltage. So, you would also need a (electrical) switch that would suddenly connect the capacitor bank to the magnet while turning “ON”.
So, the capacitor can be charged up to some high voltage with the switch being “OFF”. Next as soon as you “ON” the switch the magnet gets connected to the capacitor bank and thus all the stored charge in the bank gets dumped into the Magnet Coil – giving rise to a sudden burst of current that also dies down quickly. Thyristors are mostly used as switches for this purpose.
To analyze the circuit response, consider the R-L-C circuit (with known values of R, L and C) along with the following 2 initial conditions: current ‘I’ at time ‘t’ = 0 is zero and voltage across the capacitor bank at time t = 0 is some known value ‘Vcap’ – this is the voltage to what the capacitor bank was charged before “firing the magnet” (discharging the capacitor bank through the Magnet Coil). We assume the resistance of the connecting wires to be negligible compared to that of the magnet coil. On solving the circuit equations we arrive at the expression for the current: I(t) = (Vcap/L)*(exp[-(R/2L)t])*(sin[ωt]/ω), where: ω = [(1-d)/(L*C)]1/2 and ‘d’ is the damping coefficient: d = (R2C/4L). You will later relate the magnetic field at the centre of the bore with this current via a one-to-one mapping. Time Period: T = (1/f) = (2π/ω); “pulse width” is defined as: T0 = T/2, i.e. T0 = (2π)*(L/R)*(d/[1-d])1/2. Half of the pulse width is called the “rise time”. It denotes the time the current takes to reach its maximum value from zero.
d > 1 gives you an over-damped discharge while d < 1 leads to an under-damped discharge. The simulations below show you typical discharges of both types.
Over-damped discharge: d > 1
Under-damped discharge: d < 1
Now there is a small problem! Since ‘d’ will be determined by R, L and C values it can either be > 1 or < 1. Note how the voltage across the capacitor oscillates if d < 1! This spells danger, i.e. unsafe operating conditions! This is because, in pulsed magnetic discharges, the capacitor bank is usually constructed of paralleled electrolytic capacitors. Electrolytic capacitors give you the maximum available “capacitance and charging voltage” combination. Now, a limitation with electrolytic capacitors is that they cannot be back-charged! If the voltage across an electrolytic capacitor goes negative it will usually explode! So, to prevent this, you may fall back on a trick known as “crowbarring” that is commonly used with Pulsed Magnet circuits. You connect a diode parallel to the magnet coil.
During the negative Vc(t) cycles, the diode becomes forward-biased and carries the current, so the circuit current doesn’t flow through the capacitor bank. Rather it flows through the magnet and the diode only. Note that in the under-damped discharge simulations shown above the voltage drop across the capacitor: Vc(t) reaches zero for the first time when the circuit current I(t) just crosses its maximum. At this point the above circuit is crowbarred, i.e. the magnet coil is shorted through the forward-biased diode and is thus virtually cut-off from the capacitor bank. So, henceforth, the circuit current only decays through the magnet-diode path till it reaches zero. This is known as: the “crowbar R-L decay”. The typical behavior of a simulated crowbarred circuit is shown below.
Since a copper wire suffers a drop in its resistivity by a factor of 8 when it is submerged in Liquid Nitrogen, it would mean that the same Magnet Coil can be operated with 2 different coil resistances [at two different temperatures: room temp. and in LN2 (liquid nitrogen)]. This can lead you to a situation where the same Magnet Coil gives you an over-damped discharge when fired at room-temperature and an under-damped discharge when fired in LN2. Note that the crowbar diode can remain connected to the circuit always because even when the magnet is undergoing an over-damped discharge the presence of the diode wouldn’t harm the circuit operation.
Coil Design: Current I(t) flowing through a magnet relates directly to the magnetic field B(t) produced at the centre of the bore. You have learned that the magnetic field of a solenoid goes as: (current*# of turns/ unit length), i.e. B=(N/2b)*I. Actually this is true only if an infinitely long solenoid is assumed, where N à ∞, and b à ∞, but [N/2b] is a finite number. However, in practice, we encounter solenoids of finite length only. So, now, if a multilayer winding of finite length ‘2b’ is assumed, the field : current conversion rather becomes: B = (N/2b)*I*{F(α,β)/(α-1)}, where ‘F(α,β)’ is known as the “Field Factor”. F(α,β) = (4πβ/10)*ln[{α+(α2+β2)1/2}/{1+(1+β2)1/2}]. Since the current varies with time and because the field and the current have a one-to-one relationship, we write the dependence rather as: B(t) = [N/{2b*(α-1)}] *F(α,β) *I(t). This expression of the Field Factor considers the field B in ‘Gauss’. ‘b’ is measured in ‘cm’ and ‘I’ in ‘Ampere’. 1 Tesla = 104 Gauss.
Say you want to build a pulsed magnet now which will give you a specific combination of peak-field and rise-time. Say 20 Tesla and 5 ms. How do you go about doing it? To calculate the peak field’s expression you will need peak current’s expression which goes as: Ipeak = [Vcap*k(d)]/[(L/C)1/2], where ‘k(d)’ is known as the “Attenuation Factor” of the R-L-C circuit; k(d) = exp[(-{d/(1-d)}1/2)*tan-1({(1-d)/d}1/2)]. For all practical purposes (‘d’ varying from 10 to 10-3), k(d) lies within the range of 0.2 to 1 and is dimensionless. Bpeak can then be mapped easily to Ipeak.
There are many algorithms that can successfully lead you to the design you want. I will rather tell you the one which I follow in our Lab. It’s a graphical method and thus can be easy. Otherwise, because there are too many variables in your path, the Coil Design, by all chances, can get easily out of your hands! First, note down how many variables are there and check which of those can really be independently controlled. Here follows a list as a summary:
Independent variables: ρ, the Coil Wire’s resistivity: depends on what material it is (say, copper/ aluminium/ etc.) and also on the temperature of the Magnet Coil; wd, the (insulated) diameter of the winding wire of the Coil; a1, the bore radius/ inner radius of the Coil; α, the normalized outer radius of the multilayer winding; β, half of the normalized Coil-length; λ, the Filling Fraction; C, the capacitance of the capacitor bank; and Vcap, the voltage up to which the capacitor bank can be charged.
Dependent variables: N, the total number of turns: N = Nt*Nl = [2b/wd]*[(a2-a1)/wd]; R, the resistance of the Coil; L, the inductance of the Coil; T0, the pulse width; I, the circuit current; B, the magnetic field and σ, the stress on the wire of the Coil (which we will soon discuss).
There are other design constraints as well. Out of many let me mention 3 most important design constraints. First is the peak current. The value cannot be as high as you want it to be! So if you want a very high peak-field you should rather focus on how to increase [(N/2b)*{F(α,β)/(α-1)}]. This is because you need to pass the current through the switch – which will mostly be a thyristor, as well as through the crowbar diode, and if the individual current-carrying thresholds of the components are crossed your thyristor and diode will burn! Diodes can be put in parallel, however, to share the current. Thyristors and diodes from Semikron (stud types: www.semikron.com) have been seen to carry pulsed (in ‘ms’ range) currents up to 5 times their individual DC current ratings. Looking at the thyristor and diodes that are available with Semikron you can easily say that any peak-current value more than 10 kA will be ambitious. Second constraint will be the heat produced. The steady state (DC) “current carrying capacity” or the “current rating” of copper can well be surpassed when you are passing pulsed currents. Still, pulsed currents also have their own thresholds beyond which if you go the Coil can burn! Simply, this refers to the maximum current the wire can withstand once you have fixed its current-carrying cross-section (i.e. once wd and λ are fixed). For ‘ms’ pulses, we have regularly seen in our lab, that at room temperature, commercial copper wires can handle a load of ~ 1.8 kA/ sq. mm. We haven’t yet crossed this value. Higher this value is hotter will your magnet get after one firing. Sometimes the heat generated is so huge that one needs to wait for 10 mins to half-an-hour between two successive shots for the Magnet Coil to cool down. It’s bad to fire a hot magnet because the resistance of the coil will go up at higher temperatures leading to a lower peak field or what is worse – the coil can burn! The third constraint happens to be one of the prime obstacles to overcome. Pulsed Magnet Laboratories all over the world have struggled to produce high magnetic fields only because of this. It is the mechanical stress that is generated in the winding while firing the magnet. You know when an electrical conductor is subjected to both an electric current and a magnetic field it feels the “Lorentz force”. The winding feels this force and it is seen to be so great in Pulsed Magnet Coils that often it makes the winding cross its yield stress. The Coil then gets permanently deformed and thus the winding goes bad! However, the stress is only a concern if you want to go to peak fields beyond 30 T (with the pulse being in ‘ms’). Here, we would not discuss about issues on stress.
For the purpose of Coil Design, first choose and fix the independent variables. Copper is the most commonly used coil wire material and you can operate it at room temperature to begin with. Also note that you have virtually no control on the Filling Fraction λ because you have to buy the copper wire commercially and the insulation comes along with it: at best you can measure λ yourself – typically it will be around 0.8 to 0.9.
Note that T0, the half of which is the “rise time”, depends on ‘C’ but not on ‘Vcap’ whereas Ipeak and thus Bpeak depends on both ‘C’ and ‘Vcap’. Say there is a constraint of 10kA on Ipeak owing to the thyristor and the diode you have put. So now you need to adjust ‘C’ in such a way that you get your desired rise time and later compensate by choosing the proper ‘Vcap’ to get a high current value (within 10 kA limit). Next the Coil Geometry has to be adjusted to obtain the desired high field. For ‘ms’ pulses a ‘C’ in the ‘mF’ range will be fine. The ‘C’ value can actually be increased indefinitely by paralleling several electrolytic capacitors (that’s why it’s called a “capacitor bank”) but it’s a costly process. Each electrolytic capacitor of 4.7 mF/ 450 V will cost you around 3k INR. A ‘C’ of ~ 50 mF is welcome (around 10 such capacitors need to be paralleled: total cost 30k INR). ‘Vcap’ will be able to go up to 450 V. There are higher ‘C’ capacitors at lower prices but obviously the charging voltage will be far less than 450 V. A paralleled bank of 4.7 mF/ 450 V electrolytic capacitors is a nice starting combination for the production of high pulsed magnetic fields in the ‘ms’ range.
Let us assume that your Coil will be of copper, with a Filling Fraction of the winding wire being: λ = 0.85, and you will operate it at room temperature. Say the capacitor bank is of: C ~ 50 mF and the maximum charging voltage available is: Vcap ~ 450 V. So the maximum input energy you can feed into your pulsed magnet system is ½CV2 ~ 5 kJ. Now, after all this, virtually 4 more variables remain that can be independently tuned – all four related directly to the Coil Geometry: a1, wd, α and β. a1, the bore radius, will actually be determined by how much space you need to access within the magnet bore. In our lab we do measurements mostly on semiconductor wafers that can be cleaved to small sizes. So a bore size of ~ 1 cm works for us. Say it works for you too. That would mean: a1 ~ 0.5 cm. Now, the 3 variables that remain – wd, α and β are absolutely independent of any other constraint. Copper wires are commercially available in many gauges, so wd is available over a large range.
Next it will be wise to write a simple graph-plotting program (say in MATLAB or Mathematica) where you put in the values of: ρ, λ, C, Vcap and a1. Next put in wd as a parameter and vary α, β as the two independent variables. The program should give you back individual plots of various physical entities like the peak current, peak magnetic field, peak stress, rise-time, etc. -vs.- wd, α and β. Make sure that the (pulsed) current rating of the wire doesn’t cross your specified value (say, 1.8 kA/ sq. mm.) once both the peak current and the wire diameter have been finalized. You would see that for certain combinations of (wd, α, β) all the constraints are satisfied. This means any of these combinations can be used to design your Magnet Coil.
Design Example: Actually it’s difficult to obtain a 20T peak field at room temperature with the given constraints. You can dip the magnet coil in LN2 if you have access to LN2. It will help things immensely. Try the combination [wd = 0.295 cm (“SWG 12.5”), α = 4.5, β = 4]. It gives you a peak field of ~ 18.7 T and a rise-time of ~ 4.9 ms (with the previously mentioned parameter values, assuming the resistivity of copper at room temperature to be ρ300 K ~ 3*10-6 Ω-cm => ρLN2 ~ 0.4*10-6 Ω-cm). We see SWG 12.5 copper wire can carry a current of 13.3 kA successfully for ‘ms’ periods (from the pulsed current-capacity calculations), here we would get a peak-current of only ~ 7.7 kA. The peak stress will be ~ 1362 kg/cm2 whereas the yield stress of copper is 3500 kg/cm2. So we see that the [wd = 0.295 cm, α = 4.5, β = 4] combination works out for us. There may be several other combinations.
Last but not the least you may expect slightly less field from your coil than what is predicted by the above calculations. This is because after the discharge you will mostly see some charge remaining on the capacitor bank, i.e. the bank is not fully discharged, consequently reducing the final peak field. This happens because more often than not the magnet will be a “mismatched load” to the capacitor bank in terms of the characteristic impedance of the circuit. This issue can be tackled with more advanced methods of circuit design.
Stress expressions and calculations, and more details on Pulsed Magnets are given in the book: “Solenoid Magnet Design” by D. Bruce Montgomery (Wiley Interscience). The series: “High Magnetic Fields Science & Technology” (Vols. 1-3) edited by Fritz Herlach & Noboru Miura (World Scientific, 2003) is also an interesting read.
Some Interesting Facts: 1. ~ 21 T is believed to be the maximum steady (DC) field that a Superconducting Magnet can regularly produce. Higher magnetic fields can be achieved through Pulsed Magnets.
2. 100 T Peak Field with time period in the ms range was achieved in 1999 at Amsterdam with Pulsed Magnets.
3. Peak Fields close to 500 – 700 T can be produced with time periods in the μs/ns ranges. One common technique is to pass Mega-Amps of current through a single-turn coil (N=1): the coil is destroyed but the space inside the bore (can carry a sample) remains unharmed!
4. Design of Pulsed Magnets (especially Coil design, with a focus to keep the stress under limits) have become so critical that expensive Design Software have started to become commercially available.
5. Control of ‘Field Shape’: B(t)-vs.-t can be obtained and is known as ‘Pulse Shaping’. For e.g.- a Flat-topped Pulse can be generated by improvising the R-L-C circuit. Any other user-defined shape is also possible! Such magnets are known as ‘Controlled Waveform Magnets’ (CWMs).
Acknowledgements:
The source of all my knowledge on Pulsed Magnets are these people:
- Prof. Venki Venkataraman (http://www.physics.iisc.ernet.in/~venki),
- Dr. OVSN Murthy (http://murthyovsn.info/),
- Dr. Bhavtosh Bansal (http://www.iiserkol.ac.in/people/faculty/bhavtosh_bansal/home.html).